Bank Soal Dan Pembahasan Matematika Dasar Matriks
 Catatan calon guru yang kita diskusikan dikala ini akan membahas ihwal Matematika Dasar Matriks. Matriks menjadi salah satu topik yang paling banyak disenangi oleh siswa, sebab ialah untuk berguru matriks hanya butuh sedikit ketelitian dan kesabaran. Mempelajari dan menggunakan aturan-aturan pada matriks juga sangatlah mudah, kalau Anda mengikuti step by step yang kita diskusikan dibawah ini, maka anda akan dengan praktis memahami soal-soal matriks dan menemukan solusinya.
Catatan calon guru yang kita diskusikan dikala ini akan membahas ihwal Matematika Dasar Matriks. Matriks menjadi salah satu topik yang paling banyak disenangi oleh siswa, sebab ialah untuk berguru matriks hanya butuh sedikit ketelitian dan kesabaran. Mempelajari dan menggunakan aturan-aturan pada matriks juga sangatlah mudah, kalau Anda mengikuti step by step yang kita diskusikan dibawah ini, maka anda akan dengan praktis memahami soal-soal matriks dan menemukan solusinya.Matriks ialah susunan bilangan yang diatur menurut aturan baris dan kolom dalam suatu susunan berbentuk persegipanjang. Susunan bilangan itu diletakkan di dalam kurung biasa $"(\ \ )"$ atau kurung siku $"[\ \ ]"$.
Masing-masing bilangan dalam matriks disebut entri atau elemen. Umumnya penamaan suatu matriks dinyatakan dengan abjad kapital, misalnya $A,\ B,\ C,\ D, \cdots $ dan seterusnya.
Soal-soal yang berkembang pada matriks sering kali dikaitkan dengan materi pokok matematika lainnya, seperti: Eksponen, Bentuk Akar, Logaritma, Trigonometri, dan materi lainnya berpeluang dikaitkan dengan matriks.
Beberapa sampel soal untuk kita diskusikan kita sadur dari soal-soal SBMPTN (Seleksi Bersama Masuk Perguruan Tinggi Negeri) atau SMMPTN (Seleksi Mandiri Masuk Perguruan Tinggi Negeri) dan UN (Ujian Nasional).
Pada dasarnya pembahasan Matematika Dasar Matriks ini masih jauh dari sempurna, jadi kalau ada masukan yang sifatnya membangun silahkan disampaikan.
1. Soal SIMAK UI 2013 isyarat 333 (*Soal Lengkap)
Sebuah matriks dikatakan matriks ortogonal kalau $A^{-1}=A^{T}$.
Jika diketahui $\begin{bmatrix}
a& \frac{2}{3}& \frac{2}{3}\\
\frac{2}{3}& b& \frac{1}{3}\\
-\frac{2}{3}& -\frac{1}{3}& c
\end{bmatrix}$ adalah matriks ortogonal,
$a^{2}+b^{2}+c^{2}=...$
$\begin{align}
(A)\ & -1 \\
(B)\ & 0 \\
(C)\ & \dfrac{1}{9} \\
(D)\ & \dfrac{4}{9} \\
(E)\ & 1
\end{align}$
Seperti yang kita sampaikan diawal kalau melihat soal, sekilas kita harus menghitung invers matriks $3\times3$ kemudian kita samakan dengan transpose matriks sesuai dengan yang didefenisikan yaitu sebuah matriks dikatakan matriks ortogonal kalau $A^{-1}=A^{T}$.
Tetapi untuk anak SMA, menentukan invers matriks $3\times3$ ialah masalah baru sehingga kita butuh sedikit eksplorasi. Kita mencari penyelesaian soal diatas dengan mengikuti defenisi matriks ortogonal yaitu $A^{-1}=A^{T}$ dan sedikit eksplorasi yang menyampaikan bentuk baru yang begitu indah.
Eksplorasi yang kita lakukan yaitu:
$\begin{align}
A^{-1} &= A^{T} \\
& \text{(*kalikan dengan matriks A)} \\
A \times A^{-1} &= A \times A^{T} \\
I & = A \times A^{T}
\end{align}$
Sehingga kita peroleh persamaan;
$\begin{bmatrix}
a& \frac{2}{3}& \frac{2}{3}\\
\frac{2}{3}& b& \frac{1}{3}\\
-\frac{2}{3}& -\frac{1}{3}& c
\end{bmatrix}\times \begin{bmatrix}
a & \frac{2}{3}& -\frac{2}{3}\\
\frac{2}{3}& b& -\frac{1}{3}\\
\frac{2}{3}& \frac{1}{3}& c
\end{bmatrix}$$=\begin{bmatrix}
1& 0& 0\\
0& 1& 0\\
0& 0& 1
\end{bmatrix}$
dari perkalian matriks di atas mampu kita peroleh persamaan sebagai berikut;
$a^{2}+\dfrac{4}{9}+\dfrac{4}{9}=1 \cdots \left (pers. 1 \right )$
$\dfrac{4}{9}+b^{2}+\dfrac{1}{9}=1 \cdots \left (pers. 2 \right )$
$\dfrac{4}{9}+\dfrac{1}{9}+c^{2}=1 \cdots \left (pers. 3 \right )$
Apabila persamaan $\left (1 \right )$,$\left (2 \right )$, dan $\left (3 \right )$ kita jumlahkan,
maka akan kita peroleh persamaan berikut;
$a^{2}+b^{2}+c^{2}+\dfrac{18}{9}=3$
$a^{2}+b^{2}+c^{2}=1$
$\therefore$ Pilihan yang sesuai ialah $(E)\ 1$
2. Soal SIMAK UI 2013 isyarat 333 (*Soal Lengkap)
Jika $A=\begin{bmatrix}
4&3\\
2&5
\end{bmatrix}$ dan $A^{2}-xA+yI=\begin{bmatrix}
0 &0 \\
0& 0
\end{bmatrix}$ maka $x+y=...$
$\begin{align}
(A)\ & 9 \\
(B)\ & 14 \\
(C)\ & 19 \\
(D)\ & 23 \\
(E)\ & 25
\end{align}$
Untuk mencoba merampungkan masalah diatas, mampu kita lakukan dengan mengerjakan sedikit demi sedikit apa yang dibutuhkan,
$A^{2}=A\times A$
$A^{2}=\begin{bmatrix}
4&3\\
2&5
\end{bmatrix}\times \begin{bmatrix}
4&3\\
2&5
\end{bmatrix}$
$A^{2}=\begin{bmatrix}
22&27\\
18&31
\end{bmatrix}$
$xA=\begin{bmatrix}
4x&3x\\
2x&5x
\end{bmatrix}$
$yI=\begin{bmatrix}
y&0\\
0&y
\end{bmatrix}$
Apa yang sudah kita ketahui diatas kita substitusi ke persamaan
$A^{2}-xA+yI=\begin{bmatrix}
0 &0 \\
0& 0
\end{bmatrix}$
$\begin{bmatrix}
22&27\\
18&31
\end{bmatrix}-\begin{bmatrix}
4x&3x\\
2x&5x
\end{bmatrix}+\begin{bmatrix}
y&0\\
0&y
\end{bmatrix}$$=\begin{bmatrix}
0 &0 \\
0& 0
\end{bmatrix}$
Dari operasi matriks dan kesamaan matriks diatas, kita mampu beberapa persamaan, diantaranya:
$\begin{align}
18-2x+0 &= 0 \\
18 &= 2x \\
9 &=x \\
\hline
31-5x+y &=0 \\
31-45+y &=0 \\
-14+y &=0 \\
y &=14 \\
\hline
x+y &= 23
\end{align}$
$\therefore$ Pilihan yang sesuai ialah $(D)\ 23$
3. Soal UNBK Matematika IPS 2018 (*Soal Lengkap)
Diketahui matriks $A=\begin{pmatrix}
3 & 0\\
2 & 0
\end{pmatrix}$; $B=\begin{pmatrix}
2 & 1\\
3 & 2
\end{pmatrix}$; dan $A+B=C$. Invers matriks $C$ adalah...
$\begin{align}
(A)\ & \begin{pmatrix}
\frac{2}{5} & -\frac{1}{5} \\
-1 & 1
\end{pmatrix} \\
(B)\ & \begin{pmatrix}
1 & -\frac{1}{5} \\
-1 & \frac{2}{5}
\end{pmatrix} \\
(C)\ & \begin{pmatrix}
1 & \frac{1}{5} \\
-1 & \frac{2}{5}
\end{pmatrix} \\
(D)\ & \begin{pmatrix}
\frac{2}{5} & \frac{1}{5} \\
1 & \frac{2}{5}
\end{pmatrix} \\
(E)\ & \begin{pmatrix}
\frac{2}{5} & -1 \\
\frac{1}{5} & 1
\end{pmatrix}
\end{align}$
$C=A+B$
$C=\begin{pmatrix}
3 & 0\\
2 & 0
\end{pmatrix} + \begin{pmatrix}
2 & 1\\
3 & 2
\end{pmatrix}$
$C=\begin{pmatrix}
5 & 1\\
5 & 2
\end{pmatrix}$
$C^{-1}=\frac{1}{ad-bc}\begin{pmatrix}
d & -b\\
-c & a
\end{pmatrix}$
$C^{-1}=\frac{1}{(5)(2)-(5)(1)}\begin{pmatrix}
2 & -1\\
-5 & 5
\end{pmatrix}$
$C^{-1}=\frac{1}{5}\begin{pmatrix}
2 & -1\\
-5 & 5
\end{pmatrix}$
$C^{-1}= \begin{pmatrix}
\frac{2}{5} & -\frac{1}{5} \\
-1 & 1
\end{pmatrix}$
$\therefore$ Pilihan yang sesuai ialah $(A)\ \begin{pmatrix}
\frac{2}{5} & -\frac{1}{5} \\
-1 & 1
\end{pmatrix}$
4. Soal UNBK Matematika IPS 2018 (*Soal Lengkap)
Diketahui matriks $A=\begin{pmatrix}
1 & 3\\
2 & 4
\end{pmatrix}$; $B=\begin{pmatrix}
-3 & a\\
b & -2
\end{pmatrix}$; $C=\begin{pmatrix}
1 & -3\\
4 & 2
\end{pmatrix}$; dan $D=\begin{pmatrix}
-1 & 2\\
-2 & 1
\end{pmatrix}$.
Jika $A^{T}$ ialah transpose matriks $A$, nilai $2a+\frac{1}{2}b$ yang memenuhi persamaan $2A^{T}-B=CD$ adalah...
$\begin{align}
(A)\ & 3 \\
(B)\ & 7 \\
(C)\ & 12 \\
(D)\ & 17 \\
(E)\ & 31
\end{align}$
$CD=\begin{pmatrix}
1 & -3\\
4 & 2
\end{pmatrix} \begin{pmatrix}
-1 & 2\\
-2 & 1
\end{pmatrix}$
$CD= \begin{pmatrix}
(1)(-1)+(-3)(-2) & (1)(2)+(-3)(1)\\
(4)(-1)+(2)(-2) & (4)(2)+(2)(1)
\end{pmatrix}$
$CD= \begin{pmatrix}
-1+6 & 2-3\\
-4-4 & 8+2
\end{pmatrix}$
$CD= \begin{pmatrix}
5 & -1\\
-8 & 10
\end{pmatrix}$
$2A^{T}-B=2\begin{pmatrix}
1 & 2\\
3 & 4
\end{pmatrix}-\begin{pmatrix}
-3 & a\\
b & -2
\end{pmatrix}$
$2A^{T}-B=\begin{pmatrix}
2 & 4\\
6 & 8
\end{pmatrix}-\begin{pmatrix}
-3 & a\\
b & -2
\end{pmatrix}$
$2A^{T}-B=\begin{pmatrix}
5 & 4-a\\
6-b & 10
\end{pmatrix}$
$2A^{T}-B=CD$
$\begin{pmatrix}
5 & 4-a\\
6-b & 10
\end{pmatrix}=\begin{pmatrix}
5 & -1\\
-8 & 10
\end{pmatrix}$
Dari kesamaan dua matriks diatas kita peroleh $4-a=-1$, $a=5$ dan $6-b=-8$, $b=14$.
Nilai $2a+\frac{1}{2}b$
$ \begin{align}
2a+\frac{1}{2}b & = 2(5)+\frac{1}{2}(14) \\
& = 10+7 \\
& = 17
\end{align} $
$\therefore$ Pilihan yang sesuai ialah $(D)\ 17$
5. Soal UNBK Matematika IPA 2018 (*Soal Lengkap)
Diketahui matriks $A=\begin{pmatrix}
2 & 1\\
4 & -1
\end{pmatrix}$ dan $B=\begin{pmatrix}
4 & -1\\
1 & 1
\end{pmatrix}$. Jika $C=AB$, invers matriks $C$ ialah $C^{-1}=\cdots$
$\begin{align}
(A)\ & \begin{pmatrix}
\frac{1}{6} & -\frac{1}{30} \\
\frac{1}{2} & -\frac{3}{10}
\end{pmatrix} \\
(B)\ & \begin{pmatrix}
-\frac{1}{6} & \frac{1}{2} \\
-\frac{1}{30} & -\frac{3}{10}
\end{pmatrix} \\
(C)\ & \begin{pmatrix}
\frac{1}{6} & -\frac{1}{2} \\
-\frac{1}{30} & -\frac{3}{10}
\end{pmatrix} \\
(D)\ & \begin{pmatrix}
\frac{1}{6} & -\frac{1}{30} \\
-\frac{1}{2} & \frac{3}{10}
\end{pmatrix} \\
(E)\ & \begin{pmatrix}
-\frac{1}{6} & -\frac{1}{2} \\
-\frac{1}{30} & -\frac{3}{10}
\end{pmatrix}
\end{align}$
$C=AB$
$C=\begin{pmatrix}
2 & 1\\
4 & -1
\end{pmatrix} \begin{pmatrix}
4 & -1\\
1 & 1
\end{pmatrix}$
$C=\begin{pmatrix}
9 & -1\\
15 & -5
\end{pmatrix}$
$C^{-1}=\frac{1}{ad-bc}\begin{pmatrix}
d & -b\\
-c & a
\end{pmatrix}$
$C^{-1}=\frac{1}{(9)(-5)-(15)(-1)}\begin{pmatrix}
-5 & 1\\
-15 & 9
\end{pmatrix}$
$C^{-1}=\frac{1}{-30}\begin{pmatrix}
-5 & 1\\
-15 & 9
\end{pmatrix}$
$C^{-1}= \begin{pmatrix}
\frac{1}{6} & -\frac{1}{30} \\
\frac{1}{2} & -\frac{3}{10}
\end{pmatrix}$
$\therefore$ Pilihan yang sesuai ialah $(A)\ \begin{pmatrix}
\frac{1}{6} & -\frac{1}{30} \\
\frac{1}{2} & -\frac{3}{10}
\end{pmatrix}$
6. Soal UNBK Matematika IPA 2018 (*Soal Lengkap)
Agen perjalanan "Lombok Menawan" menyampaikan paket perjalanan wisata mirip tabel di bawah ini:
Bentuk matriks yang sesuai untuk menentukan biaya hotel tiap malam dan biaya satu daerah wisata adalah...
--- Paket I Paket II Sewa Hotel 5 6 Tempat Wisata 4 5 Biaya Total 3.100.000,00 3.000.000,00
$\begin{align}
(A)\ & \begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
5 & -6\\
-4 & 5
\end{pmatrix}\begin{pmatrix}
3.100.000 \\
3.000.000
\end{pmatrix} \\
(B)\ & \begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
5 & 6\\
4 & 5
\end{pmatrix}\begin{pmatrix}
3.100.000 \\
3.000.000
\end{pmatrix} \\
(C)\ & \begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
5 & 4\\
6 & 5
\end{pmatrix}\begin{pmatrix}
3.100.000 \\
3.000.000
\end{pmatrix} \\
(D)\ & \begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
5 & -4\\
-6 & 5
\end{pmatrix}\begin{pmatrix}
3.100.000 \\
3.000.000
\end{pmatrix} \\
(E)\ & \begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
-4 & 5\\
5 & -6
\end{pmatrix}\begin{pmatrix}
3.100.000 \\
3.000.000
\end{pmatrix}
\end{align}$
Dengan memisalkan Sewa Hotel=$x$ dan Tempat Wisata=$y$, maka tabel diatas kalau kita sajikan dalam bentuk matrik, kurang lebih mirip berikut ini;
$5x+4y=3.100.000$
$6x+5y=3.000.000$
$\begin{pmatrix}
5 & 4\\
6 & 5
\end{pmatrix}\begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
3.100.000 \\
3.000.000
\end{pmatrix}$
Untuk menerima nilai $x$ dan $y$ dalam persamaan matriks, kita coba gunakan invers matriks;
$\begin{align}
A \cdot X & = B \\
A^{-1} \cdot A \cdot X & = A^{-1} \cdot B \\
I \cdot X & = A^{-1} \cdot B \\
X & = A^{-1} \cdot B \\
\end{align} $
$\begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
5 & 4\\
6 & 5
\end{pmatrix}^{-1} \begin{pmatrix}
3.100.000 \\
3.000.000
\end{pmatrix}$
$\begin{pmatrix}
x \\
y
\end{pmatrix}=\frac{1}{(5)(5)-(6)(4)}\begin{pmatrix}
5 & -4\\
-6 & 5
\end{pmatrix} \begin{pmatrix}
3.100.000 \\
3.000.000
\end{pmatrix}$
$\begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
5 & -4\\
-6 & 5
\end{pmatrix} \begin{pmatrix}
3.100.000 \\
3.000.000
\end{pmatrix}$
$\therefore$ Pilihan yang sesuai ialah $(A)\ \begin{pmatrix}
x \\
y
\end{pmatrix}=\begin{pmatrix}
5 & -6\\
-4 & 5
\end{pmatrix}\begin{pmatrix}
3.100.000 \\
3.000.000
\end{pmatrix}$
7. Soal SBMPTN 2018 Kode 526 (*Soal Lengkap)
Jika $A=\begin{pmatrix}
a & 1\\
b & 2
\end{pmatrix}$, $B=\begin{pmatrix}
a & 1\\
1 & 0
\end{pmatrix}$ dan $AB=\begin{pmatrix}
10 & a\\
14 & b
\end{pmatrix}$. maka nilai $ab$ adalah...
$\begin{align}
(A)\ & 9 \\
(B)\ & 10 \\
(C)\ & 12 \\
(D)\ & 14 \\
(E)\ & 16
\end{align}$
$\begin{align}
AB & = \begin{pmatrix}
10 & a\\
14 & b
\end{pmatrix} \\
\begin{pmatrix}
a & 1\\
b & 2
\end{pmatrix} \begin{pmatrix}
a & 1\\
1 & 0
\end{pmatrix} & = \begin{pmatrix}
10 & a\\
14 & b
\end{pmatrix} \\
\begin{pmatrix}
a^{2}+1 & a\\
ab+2 & b
\end{pmatrix} & = \begin{pmatrix}
10 & a\\
14 & b
\end{pmatrix} \\
ab+2 & = 14 \\
ab & = 12
\end{align}$
$\therefore$ Pilihan yang sesuai ialah $(C)\ 12$
8. Soal SIMAK UI 2018 Kode 641 (*Soal Lengkap)
Diketahui $A=\begin{pmatrix}
a & -3\\
1 & d
\end{pmatrix}$, Jika $A=A^{-1}$, nilai $|a-d|$ adalah...
$\begin{align}
(A)\ & 0 \\
(B)\ & 1 \\
(C)\ & 2 \\
(D)\ & 3 \\
(E)\ & 4
\end{align}$
$\begin{pmatrix}
a & -3\\
1 & d
\end{pmatrix}=\dfrac{1}{ad+3}\begin{pmatrix}
d & 3\\
-1 & a
\end{pmatrix}$
$\begin{pmatrix}
a & -3\\
1 & d
\end{pmatrix}=\begin{pmatrix}
\dfrac{d}{ad+3} & \dfrac{3}{ad+3}\\
\dfrac{-1}{ad+3} & \dfrac{a}{ad+3}
\end{pmatrix}$
Kesimpulan yang mampu kita ambil dari kesamaan matriks diatas adalah...
$ \begin{align}
\dfrac{-1}{ad+3} & = 1 \\
-1 & = ad+3 \\
ad & = -1-3=-4
\end{align} $
$ \begin{align}
a & = \dfrac{d}{ad+3} \\
a & = \dfrac{d}{-4+3} \\
a & = -d \\
ad & = -4 \\
(-d)d & = -4 \\
-d^{2} & = -4 \\
d & = \pm \sqrt{4} =\pm 2
\end{align} $
Untuk $d=2$ maka $a=-2$
Untuk $d=-2$ maka $a=2$
Nilai $|a-d|=|2-(-2)|=4$
$\therefore$ Pilihan yang sesuai ialah $(E)\ 4$
9. Soal SIMAK UI 2009 Kode 931 (*Soal Lengkap)
Diketahui $l$ ialah garis yang dinyatakan oleh $det(A)=0$ dimana $A=\begin{pmatrix}
1 & 1 & 2\\
x & y & 1\\
2 & 1 & 3
\end{pmatrix}$, persamaan garis yang sejajar $l$ dan melalui titik $(3,4)$ adalah...
$\begin{align}
(A)\ & x+y-7=0 \\
(B)\ & x-y+7=0 \\
(C)\ & x-y+1=0 \\
(D)\ & x+y-1=0 \\
(E)\ & x+y+1=0
\end{align}$
Untuk menerima persamaan garis $l$ kita mulai dengan menentukan determinan matrisk ordo $3 \times 3$ yang nilainya ialah nol.
$0=\begin{vmatrix}
1 & 1 & 2\\
x & y & 1\\
2 & 1 & 3
\end{vmatrix}\left.\begin{matrix}
1 & 1\\
x & y\\
2 & 1
\end{matrix}\right|$
Persamaan garis $l$ adalah
$(1 \cdot y \cdot 3+1 \cdot 1 \cdot 2+2 \cdot x \cdot 1)-(2 \cdot y \cdot 2+1 \cdot 1 \cdot 1+1 \cdot x \cdot 3)=0$
$(3y+2+2x)-(4y+1+3x)=0$
$ 3y+2+2x-4y-1-3x=0$
$ 1-y-x=0$
$ 1-x=y$
Persamaan garis yang sejajar ($m_{1}=m_{2}$) dengan garis $l$ melalui $(3,4)$ adalah:
$\begin{align}
m & = -1 \\
y-y_{1} & = m(x-x_{1}) \\
y-4 & = -1(x-3) \\
y-4 & = -x+3 \\
y & = -x+7 \\
\end{align}$
$ \therefore $ Pilihan yang sesuai ialah $(A)\ x+y-7=0$
10. Soal SIMAK UI 2009 Kode 921 (*Soal Lengkap)
Diketahui $P=\begin{pmatrix}
2 & 1\\
3 & 3
\end{pmatrix}$, $Q=\begin{pmatrix}
-1 & -2\\
1 & 0
\end{pmatrix}$, dan determinan dari matriks $PQ$ ialah $k$. Jika garis $2x-y=4$ dan $3x-2y=5$ berpotongan di $A$, maka persamaan garis yang melalui $A$ dengan gradien $k$ adalah...
$\begin{align}
(A)\ & 6x+y-20=0 \\
(B)\ & 2x-3y-6=0 \\
(C)\ & 3x-2y-4=0 \\
(D)\ & x-6y+16=0 \\
(E)\ & 6x-y-16=0
\end{align}$
Unsur-unsur yang dibutuhkan untuk membentuk sebuah persamaan garis ialah sebuah titik dan gradien, $m=k=|PQ|$
$\begin{align}
m & = |PQ| \\
& = \left | \begin{pmatrix}
2 & 1\\
3 & 3
\end{pmatrix} \begin{pmatrix}
-1 & -2\\
1 & 0
\end{pmatrix} \right | \\
& = \begin{vmatrix}
-1 & -4\\
0 & -6
\end{vmatrix} \\
& = 6-0=6
\end{align}$
Titik $A$
$\begin{array}{c|c|cc}
2x-y = 4 & (\times 2) \\
3x-2y = 5 & (\times 1) \\
\hline
4x-2y = 8 & \\
3x-2y = 5 & (-) \\
\hline
x = 3 & \\
3x-2y = 5 & \\
3(3)-2y = 5 & \\
y = 2
\end{array} $
Persamaan garis melalui $A(3,2)$ dengan $m=6$
$\begin{align}
y-y_{1} & = m(x-x_{1}) \\
y-2 & = 6(x-3) \\
y & = 6x-18+2 \\
y & = 6x-16
\end{align}$
$ \therefore $ Pilihan yang sesuai ialah $(E)\ 6x-y-16=0$
11. Soal UM UGM 2014 Kode 522 (*Soal Lengkap)
Nilai semua $x$ sehingga matriks $\begin{pmatrix}
\sqrt{x^{2}-1} & 1\\
x & 2
\end{pmatrix}$, mempunyai invers adalah...
$\begin{align}
(A)\ & x \neq -\dfrac{4}{3}\ \text{dan}\ x \neq \dfrac{4}{3} \\
(B)\ & x \neq -\sqrt{\dfrac{4}{3}}\ \text{dan}\ x \neq \sqrt{\dfrac{4}{3}} \\
(C)\ & \sqrt{\dfrac{4}{3}} \lt x \leq -1\ \text{atau}\ 1 \leq x \lt \sqrt{\dfrac{4}{3}} \\
(D)\ & -\sqrt{\dfrac{4}{3}} \lt x \leq -1\ \text{atau}\ 1 \lt x \lt \sqrt{\dfrac{4}{3}} \\
(E)\ & x \lt -\sqrt{\dfrac{4}{3}}\ \text{atau}\ -\sqrt{\dfrac{4}{3}} \lt x \leq -1\ \text{atau}\ 1 \leq x \lt \sqrt{\dfrac{4}{3}}\ \text{atau}\ x \gt \sqrt{\dfrac{4}{3}}
\end{align}$
Agar sebuah matriks $\begin{pmatrix}
a & b\\
c & d
\end{pmatrix}$ mempunyai invers maka $ad-bc \neq 0$
$\begin{align}
\begin{vmatrix}
\sqrt{x^{2}-1} & 1\\
x & 2
\end{vmatrix} & \neq 0 \\
2 \sqrt{x^{2}-1} -x & \neq 0 \\
2 \sqrt{x^{2}-1} & \neq x \\
4x^{2}-4 & \neq x^{2} \\
3x^{2} & \neq 4 \\
x^{2} & \neq \dfrac{4}{3} \\
x & \neq \pm \sqrt{\dfrac{4}{3}}
\end{align}$
Syarat sebuah fungsi bentuk akar $\sqrt{f(x)}$ mempunyai nilai real ialah $f(x) \geq 0$.
Agar $\sqrt{x^{2}-1}$ mempunyai nilai real maka $x^{2}-1 \geq 0$, nilai $x$ yang memenuhi pertidaksamaan kuadrat $x^{2}-1 \geq 0$ ialah $x \leq -1\ \text{atau}\ x \geq 1$.
Jika kita gambarkan irisan $x \neq \pm \sqrt{\dfrac{4}{3}}$ dan $x \leq -1\ \text{atau}\ x \geq 1$ ialah mirip berikut ini;
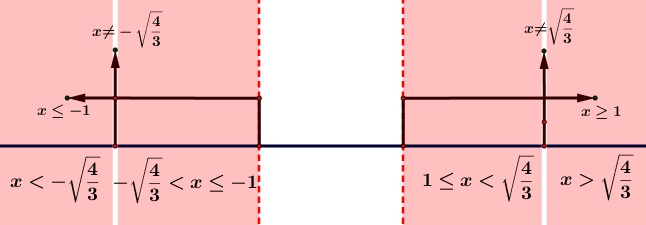
$\therefore$ Pilihan yang sesuai ialah $(E)\ x \lt -\sqrt{\dfrac{4}{3}}\ \text{atau}$ $ -\sqrt{\dfrac{4}{3}} \lt x \leq -1\ \text{atau}$ $1 \leq x \lt \sqrt{\dfrac{4}{3}}\ \text{atau}\ x \gt \sqrt{\dfrac{4}{3}}$
12. Soal UMB-PT 2014 Kode 672 (*Soal Lengkap)
Jika matriks $A=\begin{pmatrix}
a & b\\
b & a
\end{pmatrix}$, $b \neq 0$ dan $I=\begin{pmatrix}
1 & 0\\
0 & 1
\end{pmatrix}$ memenuhi $A \cdot A=A+I$, maka $b^{2}=\cdots$
$\begin{align}
(A)\ & \dfrac{5}{4} \\
(B)\ & \dfrac{3}{2} \\
(C)\ & \dfrac{7}{4} \\
(D)\ & 2 \\
(E)\ & \dfrac{9}{4} \\
\end{align}$
Karena matriks $A=\begin{pmatrix}
a & b\\
b & a
\end{pmatrix}$ memenuhi persamaan $A \cdot A=A+I$ sehingga berlaku:
$\begin{align}
\begin{pmatrix}
a & b\\
b & a
\end{pmatrix} \cdot \begin{pmatrix}
a & b\\
b & a
\end{pmatrix} & = \begin{pmatrix}
a & b\\
b & a
\end{pmatrix} + \begin{pmatrix}
1 & 0\\
0 & 1
\end{pmatrix} \\
\begin{pmatrix}
a^{2}+b^{2} & ab+ab\\
ab+ab & a^{2}+b^{2}\\
\end{pmatrix} & = \begin{pmatrix}
a+1 & b\\
b & a+1
\end{pmatrix} \\
\begin{pmatrix}
a^{2}+b^{2} & 2ab \\
2ab & a^{2}+b^{2}\\
\end{pmatrix} & = \begin{pmatrix}
a+1 & b\\
b & a+1
\end{pmatrix} \\
\hline
2ab & = b \\
a & = \dfrac{b}{2b} = \dfrac{1}{2} \\
a^{2}+b^{2} & = a+1 \\
b^{2} & = a+1-a^{2} \\
& = \dfrac{1}{2}+1-\left( \dfrac{1}{2} \right) ^{2} \\
& = \dfrac{3}{2} - \dfrac{1}{4} = \dfrac{5}{4}
\end{align}$
$\therefore$ Pilihan yang sesuai ialah $(A)\ \dfrac{5}{4}$
13. Soal SBMPTN 2014 Kode 643 (*Soal Lengkap)
Jika $A=\begin{pmatrix}
-1 & -1 & 0\\
-1 & 1 & 2
\end{pmatrix}$, $B=\begin{pmatrix}
-1 & x \\
1 & y \\
0 & z
\end{pmatrix}$ dan $AB=\begin{pmatrix}
0 & 2 \\
2 & 4
\end{pmatrix}$, maka nilai $z-x$ adalah...
$\begin{align}
(A)\ & 6 \\
(B)\ & 3 \\
(C)\ & 0 \\
(D)\ & -3 \\
(E)\ & -6
\end{align}$
$\begin{align}
\begin{pmatrix}
-1 & -1 & 0\\
-1 & 1 & 2
\end{pmatrix} \cdot \begin{pmatrix}
-1 & x \\
1 & y \\
0 & z
\end{pmatrix} & = \begin{pmatrix}
0 & 2 \\
2 & 4
\end{pmatrix} \\
\begin{pmatrix}
1-1+0 & -x -y+0\\
1+1+0 & -x+y+2z
\end{pmatrix} & = \begin{pmatrix}
0 & 2 \\
2 & 4
\end{pmatrix} \\
\begin{pmatrix}
0 & -x -y \\
2 & -x+y+2z
\end{pmatrix} & = \begin{pmatrix}
0 & 2 \\
2 & 4
\end{pmatrix}
\end{align}$
Dari kesamaan dua matriks di atas kita peroleh:
$\begin{array}{c|c|cc}
-x-y=2 & \\
-x+y+2z = 4 & (+) \\
\hline
-2x+2z = 6 & \\
-x+z = 3
\end{array} $
$\therefore$ Pilihan yang sesuai ialah $(B)\ 3$
14. Soal SBMPTN 2014 Kode 613 (*Soal Lengkap)
Jika $\begin{pmatrix}
y \\
x
\end{pmatrix}=\begin{pmatrix}
2 & 1 \\
-1 & x
\end{pmatrix}^{-1} \begin{pmatrix}
4 \\
-1
\end{pmatrix}$ dengan $x \neq \dfrac{1}{2}$, maka nilai $\dfrac{1}{2}x+y=\cdots$
$\begin{align}
(A)\ & -4 \\
(B)\ & -2 \\
(C)\ & 0 \\
(D)\ & 2 \\
(E)\ & 4
\end{align}$
Kita mengetahui sifat perkalian matriks yaitu kalau $A=B^{-1} \cdot C$ maka $BA=C$.
$\begin{align}
\begin{pmatrix}
y \\
x
\end{pmatrix} & = \begin{pmatrix}
2 & 1 \\
-1 & x
\end{pmatrix}^{-1} \begin{pmatrix}
4 \\
-1
\end{pmatrix} \\
\begin{pmatrix}
2 & 1 \\
-1 & x
\end{pmatrix} \begin{pmatrix}
y \\
x
\end{pmatrix} & = \begin{pmatrix}
4 \\
-1
\end{pmatrix} \\
\begin{pmatrix}
2y+x \\
-y+x^{2}
\end{pmatrix} & = \begin{pmatrix}
4 \\
-1
\end{pmatrix}
\end{align}$
Dari kesamaan dua matriks di atas kita peroleh $2y+x=4$ sehingga $ y+\dfrac{1}{2}x=2$
$\therefore$ Pilihan yang sesuai ialah $(D)\ 2$
15. Soal SBMPTN 2014 Kode 601 (*Soal Lengkap)
Jika $P=\begin{pmatrix}
1 & 2 \\
1 & 3
\end{pmatrix}$ dan $\begin{pmatrix}
x & y \\
-z & z
\end{pmatrix}=2P^{-1}$ dengan $P^{-1}$ menyatakan invers matriks $P$, maka $x+y=\cdots$
$\begin{align}
(A)\ & 0 \\
(B)\ & 1 \\
(C)\ & 2 \\
(D)\ & 3 \\
(E)\ & 4
\end{align}$
Invers sebuah matriks $A= \begin{pmatrix}
a & b\\
c & d
\end{pmatrix}$ ialah $A^{-1}=\frac{1}{ad-bc}\begin{pmatrix}
d & -b\\
-c & a
\end{pmatrix}$
$\begin{align}
P & = \begin{pmatrix}
1 & 2 \\
1 & 3
\end{pmatrix} \\
P^{-1} & = \frac{1}{(1)(3)-(2)(1)}\begin{pmatrix}
3 & -2\\
-1 & 1
\end{pmatrix} \\
\dfrac{1}{2}\begin{pmatrix}
x & y \\
-z & z
\end{pmatrix} & = \begin{pmatrix}
3 & -2\\
-1 & 1
\end{pmatrix}
\end{align}$
Dari kesamaan dua matriks di atas kita peroleh $\dfrac{1}{2}x=3$ dan $\dfrac{1}{2}y=-2$ sehingga $x+y=2$
$\therefore$ Pilihan yang sesuai ialah $(C)\ 2$
16. Soal SBMPTN 2014 Kode 631 (*Soal Lengkap)
Jika $A=\begin{pmatrix}
2 & 3 \\
-1 & 1
\end{pmatrix}$, $B$ memiliki invers, dan $ \left( AB^{-1} \right)^{-1}= \begin{pmatrix}
1 & -1 \\
3 & 0
\end{pmatrix}$ maka matriks $B=\cdots$
$\begin{align}
(A)\ & \begin{pmatrix}
4 & -1 \\
6 & 1
\end{pmatrix} \\
(B)\ & \begin{pmatrix}
3 & 2 \\
6 & 9
\end{pmatrix} \\
(C)\ & \begin{pmatrix}
2 & 0 \\
0 & 1
\end{pmatrix} \\
(D)\ & \begin{pmatrix}
1 & 6 \\
4 & 3
\end{pmatrix} \\
(E)\ & \begin{pmatrix}
4 & 5 \\
6 & -5
\end{pmatrix}
\end{align}$
Sifat perkalian invers pada matriks berlaku $(AB)^{-1}=B^{-1} \cdot A^{-1}$.
$\begin{align}
\left( AB^{-1} \right)^{-1} & = \begin{pmatrix}
1 & -1 \\
3 & 0
\end{pmatrix} \\
B \cdot A^{-1} & = \begin{pmatrix}
1 & -1 \\
3 & 0
\end{pmatrix} \\
B \cdot A^{-1} \cdot A & = \begin{pmatrix}
1 & -1 \\
3 & 0
\end{pmatrix} \cdot A \\
B & = \begin{pmatrix}
1 & -1 \\
3 & 0
\end{pmatrix} \cdot \begin{pmatrix}
2 & 3 \\
-1 & 1
\end{pmatrix} \\
& = \begin{pmatrix}
2+1 & 3-1 \\
6+0 & 9+0
\end{pmatrix} \\
& = \begin{pmatrix}
3 & 2 \\
6 & 9
\end{pmatrix}
\end{align}$
$\therefore$ Pilihan yang sesuai ialah $(B)\ \begin{pmatrix}
3 & 2 \\
6 & 9
\end{pmatrix}$
17. Soal SBMPTN 2014 Kode 673 (*Soal Lengkap)
Diketahui matriks $A=\begin{pmatrix}
1 & 2 \\
3 & 4
\end{pmatrix}$, dan $B= \begin{pmatrix}
1 & y \\
x & 3
\end{pmatrix}$. Jika determinan $AB$ ialah $10$, maka $xy=\cdots$
$\begin{align}
(A)\ & 4 \\
(B)\ & 6 \\
(C)\ & 8 \\
(D)\ & 10 \\
(E)\ & 12
\end{align}$
$\begin{align}
AB & = \begin{pmatrix}
1 & 2 \\
3 & 4
\end{pmatrix} \begin{pmatrix}
1 & y \\
x & 3
\end{pmatrix} \\
& = \begin{pmatrix}
1+2x & y+6 \\
3+4x & 3y+12
\end{pmatrix} \\
|AB| & = \begin{vmatrix}
1+2x & y+6 \\
3+4x & 3y+12
\end{vmatrix} \\
10 & = (1+2x)(3y+12)-(y+6)(3+4x) \\
10 & = 3y+12+6xy+24x -3y-4xy-18-24x \\
10 & = 2xy -6 \\
10+6 & = 2xy \\
8 & = xy
\end{align}$
$\therefore$ Pilihan yang sesuai ialah $(C)\ 8$
18. Soal SBMPTN 2014 Kode 673 (*Soal Lengkap)
Jika $\begin{pmatrix}
a & b \\
b & 2a
\end{pmatrix}\begin{pmatrix}
x \\
x+y
\end{pmatrix}=\begin{pmatrix}
a \\
b
\end{pmatrix}$ dengan $b^{2} \neq 2a^{2}$, maka $x+y=\cdots$
$\begin{align}
(A)\ & -2 \\
(B)\ & -1 \\
(C)\ & 0 \\
(D)\ & 1 \\
(E)\ & 2
\end{align}$
$\begin{align}
\begin{pmatrix}
a & b \\
b & 2a
\end{pmatrix}\begin{pmatrix}
x \\
x+y
\end{pmatrix} &= \begin{pmatrix}
a \\
b
\end{pmatrix} \\
\begin{pmatrix}
ax+bx+by \\
bx+2ax+2ay
\end{pmatrix} &= \begin{pmatrix}
a \\
b
\end{pmatrix}
\end{align}$
Dari kesamaan dua matriks di atas kita peroleh:
$\begin{array}{c|c|cc}
ax+bx+by=a & (\times b)\\
bx+2ax+2ay=b & (\times a) \\
\hline
abx+b^{2}x+b^{2}y=ab & \\
abx+2a^{2}x+2a^{2}y=ab & (-) \\
\hline
b^{2}x+b^{2}y-2a^{2}x+2a^{2}y=0 \\
\left( b^{2} -2a^{2} \right) x+ \left( b^{2} -2a^{2} \right)y=0 \\
\left( b^{2} -2a^{2} \right) \left( x+y \right) =0 \\
\left( x+y \right) = \dfrac{0}{\left( b^{2} -2a^{2} \right)} \\
\left( x+y \right) = 0
\end{array} $
$\therefore$ Pilihan yang sesuai ialah $(C)\ 0$
19. Soal SBMPTN 2014 Kode 663 (*Soal Lengkap)
Jika matriks $A=\begin{pmatrix}
2x & -2 \\
x & 3y+2
\end{pmatrix}$, $B=\begin{pmatrix}
9 & 3x \\
8 & -4
\end{pmatrix}$ dan $C=\begin{pmatrix}
5 & 6 \\
-8 & 7
\end{pmatrix}$ memenuhi $A+B=C^{t}$ dengan $C^{t}$ transpose matriks $C$, maka $2x+3y=\cdots$
$\begin{align}
(A)\ & 3 \\
(B)\ & 4 \\
(C)\ & 5 \\
(D)\ & 6 \\
(E)\ & 7
\end{align}$
$\begin{align}
A+B &= C^{t} \\
\begin{pmatrix}
2x & -2 \\
x & 3y+2
\end{pmatrix}+\begin{pmatrix}
9 & 3x \\
8 & -4
\end{pmatrix} &= \begin{pmatrix}
5 & -8 \\
6 & 7
\end{pmatrix} \\
\begin{pmatrix}
2x+9 & -2+3x \\
x+8 & 3y-2
\end{pmatrix} &= \begin{pmatrix}
5 & -8 \\
6 & 7
\end{pmatrix} \\
\end{align}$
Dari kesamaan dua matriks di atas kita peroleh:
- $x+8=6$ sehingga $x=-2$
- $3y-2=7$ sehingga $y=3$
- $2x+3y=2(-2)+3(3)=-4+9=5$
$\therefore$ Pilihan yang sesuai ialah $(C)\ 5$
20. Soal SIMAK UI 2013 Kode 334 (*Soal Lengkap)
Jumlah semua entri pada matriks $X$ dari sistem persamaan berikut adalah...
$3X-2Y=\begin{bmatrix}
3 & -1
\end{bmatrix}$
$2X-5Y=\begin{bmatrix}
1 & 2
\end{bmatrix}$
$\begin{align}
(A)\ & \dfrac{13}{11} \\
(B)\ & \dfrac{9}{11} \\
(C)\ & \dfrac{8}{11} \\
(D)\ & \dfrac{5}{11} \\
(E)\ & \dfrac{4}{11}
\end{align}$
Matriks $X$ dan $Y$ ialah matriks berordo $1 \times 2$ sebab ialah hasil pengurangan matriks tersebut ialah sebuah matriks berordo $1 \times 2$. Sehingga mampu kita misalkan $X=\begin{bmatrix}
a & b
\end{bmatrix}$ dan $Y=\begin{bmatrix}
c & d
\end{bmatrix}$
$\begin{align}
3X-2Y &= \begin{bmatrix}
3 & -1
\end{bmatrix} \\
3\begin{bmatrix}
a & b
\end{bmatrix}-2\begin{bmatrix}
c & d
\end{bmatrix} &= \begin{bmatrix}
3 & -1
\end{bmatrix} \\
\begin{bmatrix}
3a-2c & 3b-2d
\end{bmatrix} &= \begin{bmatrix}
3 & -1
\end{bmatrix} \\
\hline
2X-5Y &= \begin{bmatrix}
1 & 2
\end{bmatrix} \\
2\begin{bmatrix}
a & b
\end{bmatrix}-5\begin{bmatrix}
c & d
\end{bmatrix} &= \begin{bmatrix}
1 & 2
\end{bmatrix} \\
\begin{bmatrix}
2a-5c & 2b-5d
\end{bmatrix} &= \begin{bmatrix}
1 & 2
\end{bmatrix}
\end{align}$
Dari kesamaan dua matriks di atas kita peroleh:
- $3a-2c=3$ dan $2a-5c=1$
- $3b-2d=-1$ dan $2b-5d=2$
3a-2c=3 & 3b-2d=-1 & \times 5 \\
2a-5c=1 & 2b-5d=2 & \times 2 \\
\hline
15a-10c=15 & 15b-10d=-5 & \\
4a-10c=2 & 4b-10d=4 & - \\
\hline
11a =13 & 11b =-9 & \\
a =\dfrac{13}{11} & b =\dfrac{-9}{11}
\end{array} $
Jumlah semua entri pada matriks $X$ ialah $a+b=\dfrac{4}{11}$
$\therefore$ Pilihan yang sesuai ialah $(E)\ \dfrac{4}{11}$
21. Soal SIMAK UI 2013 Kode 334 (*Soal Lengkap)
Diberikan matriks $A,\ B,\ C,\ \text{dan}\ D$ berikut ini.
$A=\begin{bmatrix}
2 & 1 \\
0 & 1
\end{bmatrix}$; $B=\begin{bmatrix}
0 & 1 \\
0 & 1
\end{bmatrix}$; $C=\begin{bmatrix}
2 & 1 \\
0 & 0
\end{bmatrix}$; $D=\begin{bmatrix}
2 & 0 \\
0 & 1
\end{bmatrix}$. Jika $x,\ y,\ z,\ \text{dan}\ w$ secara berurutan ialah jumlah entri-entri pada matriks $A^{2013},\ B^{2013},\ C^{2013},\ \text{dan}\ D^{2013}$, pernyataan-pernyataan berikut yang BENAR adalah...
$\begin{align}
(1)\ & w-1=y^{2013} \\
(2)\ & z=3y^{2012} \\
(3)\ & 4z=3x \\
(4)\ & 2w-x=2
\end{align}$
Sebagai tahap awal kita coba uji nilai untuk $A^{2}$ dan $A^{3}$
$\begin{align}
A^{2} &= \begin{bmatrix}
2 & 1 \\
0 & 1
\end{bmatrix}^{2}=\begin{bmatrix}
4 & 3 \\
0 & 1
\end{bmatrix}=(8)\\
A^{3} &= \begin{bmatrix}
2 & 1 \\
0 & 1
\end{bmatrix}^{3}=\begin{bmatrix}
8 & 7 \\
0 & 1
\end{bmatrix}=(16) \\
A^{4} &= \begin{bmatrix}
2 & 1 \\
0 & 1
\end{bmatrix}^{4}\begin{bmatrix}
16 & 15 \\
0 & 1
\end{bmatrix}=(32) \\
x &= 2^{2013+1} \\
\hline
B^{2} &= \begin{bmatrix}
0 & 1 \\
0 & 1
\end{bmatrix}^{2}=\begin{bmatrix}
0 & 1 \\
0 & 1
\end{bmatrix}=(2) \\
B^{3} &= \begin{bmatrix}
0 & 1 \\
0 & 1
\end{bmatrix}^{3}=\begin{bmatrix}
0 & 1 \\
0 & 1
\end{bmatrix}=(2) \\
y &= 2 \\
\hline
C^{2} &= \begin{bmatrix}
2 & 1 \\
0 & 0
\end{bmatrix}^{2}=\begin{bmatrix}
4 & 2 \\
0 & 0
\end{bmatrix}=(6) \\
C^{3} &= \begin{bmatrix}
2 & 1 \\
0 & 0
\end{bmatrix}^{3}=\begin{bmatrix}
8 & 4 \\
0 & 0
\end{bmatrix}=(12) \\
C^{4} &= \begin{bmatrix}
2 & 1 \\
0 & 0
\end{bmatrix}^{4}=\begin{bmatrix}
16 & 8 \\
0 & 0
\end{bmatrix}=(24) \\
z &= 2^{2013-1} \cdot 3 \\
\hline
D^{2} &= \begin{bmatrix}
2 & 0 \\
0 & 1
\end{bmatrix}^{2}=\begin{bmatrix}
4 & 0 \\
0 & 1
\end{bmatrix}=(5) \\
D^{3} &= \begin{bmatrix}
2 & 0 \\
0 & 1
\end{bmatrix}^{3}=\begin{bmatrix}
8 & 0 \\
0 & 1
\end{bmatrix}=(9) \\
D^{4} &= \begin{bmatrix}
2 & 0 \\
0 & 1
\end{bmatrix}^{4}=\begin{bmatrix}
16 & 0 \\
0 & 1
\end{bmatrix}=(17) \\
w &= 2^{2013}+1 \\
\end{align}$
Dari nilai $x=2^{2014},\ y=2,\ z=3 \cdot 2^{2012},\ \text{dan}\ w=1+2^{2013}$ yang kita peroleh di atas, maka mampu kita simpulkan:
- $(1)\ w-1=y^{2013}$ Benar
- $(2)\ z=3y^{2012}$ Benar
- $(3)\ 4z=3x$ Benar
- $(4)\ 2w-x=2$ Benar
22. Soal SIMAK UI 2013 Kode 333 (*Soal Lengkap)
Sebuah matriks dikatakan matriks ortogonal kalau $A^{-1}=A^{T}$.
Jika diketahui $\begin{bmatrix}
\frac{3}{7} & \frac{2}{7} & a \\
b & \frac{3}{7} & \frac{2}{7}\\
\frac{2}{7}& \frac{6}{7}& c
\end{bmatrix}$ adalah matriks ortogonal,
$a^{2}+b^{2}+c^{2}=...$
$\begin{align}
(A)\ & \dfrac{81}{49} \\
(B)\ & \dfrac{72}{49} \\
(C)\ & \dfrac{45}{49} \\
(D)\ & \dfrac{36}{49} \\
(E)\ & \dfrac{9}{49}
\end{align}$
Seperti yang kita sampaikan diawal kalau melihat soal, sekilas kita harus menghitung invers matriks $3\times3$ kemudian kita samakan dengan transpose matriks sesuai dengan yang didefenisikan yaitu sebuah matriks dikatakan matriks ortogonal kalau $A^{-1}=A^{T}$.
Tetapi untuk anak SMA, menentukan invers matriks $3\times3$ ialah masalah baru sehingga kita butuh sedikit eksplorasi. Kita mencari penyelesaian soal diatas dengan mengikuti defenisi matriks ortogonal yaitu $A^{-1}=A^{T}$ dan sedikit eksplorasi yang menyampaikan bentuk baru yang begitu indah.
Eksplorasi yang kita lakukan yaitu:
$\begin{align}
A^{-1} &= A^{T} \\
& \text{(*kalikan dengan matriks A)} \\
A \times A^{-1} &= A \times A^{T} \\
I & = A \times A^{T}
\end{align}$
Sehingga kita peroleh persamaan;
$\begin{bmatrix}
\frac{3}{7} & \frac{2}{7} & a \\
b & \frac{3}{7} & \frac{2}{7}\\
\frac{2}{7}& \frac{6}{7}& c
\end{bmatrix} \times
\begin{bmatrix}
\frac{3}{7} & b & \frac{2}{7} \\
\frac{2}{7} & \frac{3}{7} & \frac{6}{7}\\
a & \frac{2}{7}& c
\end{bmatrix}$$=\begin{bmatrix}
1& 0& 0\\
0& 1& 0\\
0& 0& 1
\end{bmatrix}$
dari perkalian matriks di atas mampu kita peroleh persamaan sebagai berikut;
$\dfrac{9}{49}+\dfrac{4}{49}+a^{2} =1 \cdots \left (pers. 1 \right )$
$b^{2}+\dfrac{9}{49}+\frac{4}{49}=1 \cdots \left (pers. 2 \right )$
$\dfrac{4}{49}+\dfrac{36}{49}+c^{2}=1 \cdots \left (pers. 3 \right )$
Apabila persamaan $\left (1 \right )$,$\left (2 \right )$, dan $\left (3 \right )$ kita jumlahkan,
maka akan kita peroleh persamaan berikut;
$a^{2}+b^{2}+c^{2}+\frac{66}{49}=3$
$a^{2}+b^{2}+c^{2}=\dfrac{147}{49}-\dfrac{66}{49}$
$a^{2}+b^{2}+c^{2}=\dfrac{81}{49}$
$\therefore$ Pilihan yang sesuai ialah $(A)\ \dfrac{81}{49}$
23. Soal UM STIS 2011 (*Soal Lengkap)
Matriks $B$ ialah invers matriks $A$, matriks $D$ ialah invers matriks $C$ dan $A \cdot B \cdot C=D$, maka yang merupakan matriks identitas $(I)$ adalah...
$\begin{align}
(A)\ & A^{2} \\
(B)\ & B^{2} \\
(C)\ & C^{2} \\
(D)\ & D^{2} \\
(E)\ & A \cdot C^{2}
\end{align}$
Catatan calon guru ihwal invers matriks mampu membantu;
- $ (A^{-1})^{-1} = A $
- $ A^{-1} . A = A.A^{-1} = I $
- $ AB = I \, $ artinya A dan B saling invers yaitu $ A^{-1} = B \, $ dan $ B^{-1} = A $
- $ (AB)^{-1} = B^{-1} . A^{-1} $
- $ B= A^{-1}$ maka $ B^{-1}=A$
- $ D= C^{-1}$ maka $ D^{-1}=C$
A \cdot B \cdot C & =D \\
A \cdot A^{-1} \cdot C & = C^{-1} \\
I \cdot C & = C^{-1} \\
C & = C^{-1} \\
C \cdot C & = C^{-1} \cdot C\\
C^{2} &= I
\end{align}$
$\begin{align}
A \cdot B \cdot C & =D \\
B^{-1} \cdot B \cdot C & = D \\
I \cdot D^{-1} & = D \\
D^{-1} & = D \\
D^{-1} \cdot D & = D \cdot D\\
I & = D^{2} \\
\end{align}$
$\therefore$ Pilihan yang sesuai ialah $(C)\ C^{2}$ atau $(D)\ D^{2}$
24. Soal UM STIS 2011 (*Soal Lengkap)
Jika $\begin{pmatrix}
a-b & -b \\
0 & 1
\end{pmatrix}^{-1}=\begin{pmatrix}
a & 1 \\
-a+2b & 1
\end{pmatrix}$ maka $ab=\cdots$
$\begin{align}
(A)\ & 2 \\
(B)\ & 1 \\
(C)\ & -\dfrac{1}{2} \\
(D)\ & -1 \\
(E)\ & -4
\end{align}$
Catatan calon guru ihwal invers matriks $2 \times 2$ berikut ini mungkin membantu;
Misalkan matriks $ A = \left( \begin{matrix} a & b \\ c & d \end{matrix} \right) $
$det(A) = |A| = $$ a \times d - b\times c $
invers matriks $A$ ialah $ A^{-1} = \frac{1}{|A|} \left( \begin{matrix} d & -b \\ -c & a \end{matrix} \right) $
$\begin{align}
\begin{pmatrix}
a-b & -b \\
0 & 1
\end{pmatrix}^{-1} & =\begin{pmatrix}
a & 1 \\
-a+2b & 1
\end{pmatrix} \\
\dfrac{1}{(a-b)-0} \begin{pmatrix}
1 & b \\
0 & a-b
\end{pmatrix} & =\begin{pmatrix}
a & 1 \\
-a+2b & 1
\end{pmatrix} \\
\begin{pmatrix}
\dfrac{1}{ a-b } & \dfrac{b}{ a-b } \\
0 & 1
\end{pmatrix} & =\begin{pmatrix}
a & 1 \\
-a+2b & 1
\end{pmatrix}
\end{align}$
Dari kesamaan dua matriks di atas kita peroleh:
- $-a+2b=0$ sehingga $a=2b$
- $\dfrac{1}{ a-b }=a$ sehingga $\dfrac{1}{ 2b-b }=a$
$\dfrac{1}{ b }=a$
$1=ab$
$\therefore$ Pilihan yang sesuai ialah $(B)\ 1$
25. Soal UM STIS 2011 (*Soal Lengkap)
Jika matriks $M$ berordo $2 \times 2$ sehingga $M \begin{pmatrix}
1 \\
-1
\end{pmatrix} =\begin{pmatrix}
-1 \\
5
\end{pmatrix}$ dan $M \begin{pmatrix}
2 \\
1
\end{pmatrix} =\begin{pmatrix}
4 \\
7
\end{pmatrix}$ maka $M^{2}=\cdots$
$\begin{align}
(A)\ & \begin{pmatrix}
1 & 2 \\
4 & -1
\end{pmatrix} \\
(B)\ & \begin{pmatrix}
9 & 0 \\
0 & 9
\end{pmatrix} \\
(C)\ & \begin{pmatrix}
9 & 0 \\
0 & 7
\end{pmatrix} \\
(D)\ & \begin{pmatrix}
7 & 0 \\
0 & 9
\end{pmatrix} \\
(E)\ & \begin{pmatrix}
7 & 0 \\
0 & 7
\end{pmatrix}
\end{align}$
Catatan calon guru ihwal Perkalian matriks berikut ini mungkin membantu;
$ \begin{align}
AB & = \left( \begin{matrix} a & b \\ c & d \end{matrix} \right) \left( \begin{matrix} e & f \\ g & h \end{matrix} \right) \\
& = \left( \begin{matrix} \text{baris 1 } \times \text{ kolom 1} & \text{baris 1 } \times \text{ kolom 2} \\ \text{baris 2 } \times \text{ kolom 1} & \text{baris 2 } \times \text{ kolom 2}\end{matrix} \right) \\
& = \left( \begin{matrix} a.e+b.g & a.f + b.h \\ c.e + d.g & c.f + d.h \end{matrix} \right)
\end{align} $
Kita coba dengan memisalkan matriks $M=\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}$
$\begin{align}
M \begin{pmatrix}
1 \\
-1
\end{pmatrix} & =\begin{pmatrix}
-1 \\
5
\end{pmatrix} \\
\begin{pmatrix}
a & b \\
c & d
\end{pmatrix} \begin{pmatrix}
1 \\
-1
\end{pmatrix} & =\begin{pmatrix}
-1 \\
5
\end{pmatrix} \\
\begin{pmatrix}
a-b \\
c-d
\end{pmatrix} & =\begin{pmatrix}
-1 \\
5
\end{pmatrix} \\
\hline
M \begin{pmatrix}
2 \\
1
\end{pmatrix} & =\begin{pmatrix}
4 \\
7
\end{pmatrix} \\
\begin{pmatrix}
a & b \\
c & d
\end{pmatrix} \begin{pmatrix}
2 \\
1
\end{pmatrix} & =\begin{pmatrix}
4 \\
7
\end{pmatrix} \\
\begin{pmatrix}
2a+b \\
2c+d
\end{pmatrix} & =\begin{pmatrix}
4 \\
7
\end{pmatrix}
\end{align}$
Dari kesamaan dua matriks di atas kita peroleh;
$\begin{array}{c|c|cc}
a-b = -1 & c-d = 5 & \\
2a+b = 4 & 2c+d = 7 & + \\
\hline
3a = 3 & 3c = 12 \\
a = 1 & c = 4 \\
b = 2 & d = -1
\end{array} $
$M=\begin{pmatrix}
1 & 2 \\
4 & -1
\end{pmatrix}$ maka $M^{2}=\begin{pmatrix}
9 & 0 \\
0 & 9
\end{pmatrix}$
$\therefore$ Pilihan yang sesuai ialah $(B)\ \begin{pmatrix}
9 & 0 \\
0 & 9
\end{pmatrix}$
26. Soal UM STIS 2011 (*Soal Lengkap)
Diketahui matriks $A =\begin{pmatrix}
2 & 4 \\
2b & 3c
\end{pmatrix}$ dan $B=\begin{pmatrix}
2c-3b & 2a+1 \\
a & b+7
\end{pmatrix}$. Jika $B^{T}$ ialah transpose dari matriks $B$, maka nilai $c$ yang memenuhi $A=2B^{T}$ adalah...
$\begin{align}
(A)\ & 2 \\
(B)\ & 3 \\
(C)\ & 5 \\
(D)\ & 8 \\
(E)\ & 10
\end{align}$
Catatan calon guru ihwal Transpose matriks berikut ini mungkin membantu;
Jika $A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$ maka $A^{T} = \begin{pmatrix} a & c \\ b & d \end{pmatrix}$
$\begin{align}
A & = 2B^{T} \\
\begin{pmatrix}
2 & 4 \\
2b & 3c
\end{pmatrix} & = 2 \begin{pmatrix}
2c-3b & a \\
2a+1 & b+7
\end{pmatrix} \\
\begin{pmatrix}
2 & 4 \\
2b & 3c
\end{pmatrix} & = \begin{pmatrix}
4c-6b & 2a \\
4a+2 & 2b+14
\end{pmatrix}
\end{align}$
Dari kesamaan dua matriks di atas kita peroleh;
- $2= 4c-6b$
- $4=2a$ maka $a=2$
- $2b=4a+2$ maka $2b=8+2 $, $b=5$
- $3c=2b+14$ maka $3c=10+14$, $c=8$
27. Soal UNBK Matematika IPA 2019 (*Soal Lengkap)
Diketahui persamaan matriks $\begin{pmatrix}
a & b\\
1 & 3
\end{pmatrix}\begin{pmatrix}
2 & 1\\
4 & -2
\end{pmatrix}=\begin{pmatrix}
8 & 12\\
14 & -5
\end{pmatrix}$. Nilai $2a-b=\cdots$
$\begin{align}
(A)\ & 18 \\
(B)\ & 16 \\
(C)\ & 14 \\
(D)\ & 10 \\
(E)\ & 6
\end{align}$
Berdasarkan gosip pada soal perkalian matriks di atas, maka berlaku:
$\begin{align}
\begin{pmatrix}
a & b\\
1 & 3
\end{pmatrix}\begin{pmatrix}
2 & 1\\
4 & -2
\end{pmatrix} &= \begin{pmatrix}
8 & 12\\
14 & -5
\end{pmatrix} \\
\begin{pmatrix}
2a+4b & a-2b\\
2+12 & 1-6
\end{pmatrix} &= \begin{pmatrix}
8 & 12\\
14 & -5
\end{pmatrix}
\end{align} $
$\begin{array}{c|c|cc}
2a+4b = 8 & \times 1 \\
a-2b = 12 & \times 2 \\
\hline
2a+4b = 8 & \\
2a-4b = 24 & (+)\\
\hline
4a=32 \\
a=8 \\
b=-2
\end{array} $
Nilai $2a-b=2(8)-(-2)=18$
$\therefore$ Pilihan yang sesuai ialah $(A)\ 18$
28. Soal UTBK Tes Kompetensi Akademik SAINTEK 2019
Diketahui matriks $B=\begin{pmatrix}
1 & -4\\
5 & -2
\end{pmatrix}$ dan berlaku persamaan $A^{2}+B=\begin{pmatrix}
3 & -2\\
4 & -1
\end{pmatrix}$. Determinan matriks $A^{4}$ adalah...
$\begin{align}
(A)\ & 1 \\
(B)\ & 2 \\
(C)\ & 4 \\
(D)\ & 16 \\
(E)\ & 81
\end{align}$
Berdasarkan gosip pada penjumlahan matriks soal di atas, maka berlaku:
$\begin{align}
A^{2}+B &=\begin{pmatrix}
3 & -2\\
4 & -1
\end{pmatrix} \\
A^{2} &=\begin{pmatrix}
3 & -2\\
4 & -1
\end{pmatrix}-B \\
A^{2} &=\begin{pmatrix}
3 & -2\\
4 & -1
\end{pmatrix}-\begin{pmatrix}
1 & -4\\
5 & -2
\end{pmatrix}\\
A^{2} &=\begin{pmatrix}
3-1 & -2+4\\
4-5 & -1+2
\end{pmatrix} \\
A^{2} &=\begin{pmatrix}
2 & 2 \\
-1 & 1
\end{pmatrix} \\
\left| A^{2} \right| &=(2)(1)-(-1)(2)=4 \\
\end{align} $
Dengan mengunakan sifat determinan matriks $\left| A^{n} \right| = \left | A \right | ^{n}$ maka:
$\begin{align}
\left| A^{4} \right| &= \left| A^{2} \right|^{2} \\
&= 4^{2} =16
\end{align} $
$\therefore$ Pilihan yang sesuai ialah $(D)\ 16$
29. Soal UTBK Tes Kompetensi Akademik SAINTEK 2019
Diketahui matriks $A$ berukuran $2 \times 2$ dan $B=\begin{pmatrix}
-1 & 3\\
0 & 2
\end{pmatrix}$. Jika $B-A=\begin{pmatrix}
2 & -1\\
1 & 0
\end{pmatrix}$ maka $det \left( 2A^{-1} \right)$ adalah...
$\begin{align}
(A)\ & -4 \\
(B)\ & -2 \\
(C)\ & -1 \\
(D)\ & 1 \\
(E)\ & 2
\end{align}$
Berdasarkan gosip pada pengurangan matriks soal di atas, maka berlaku:
$\begin{align}
B-A &=\begin{pmatrix}
2 & -1\\
1 & 0
\end{pmatrix} \\
B-\begin{pmatrix}
2 & -1\\
1 & 0
\end{pmatrix} &= A \\
\begin{pmatrix}
-1 & 3\\
0 & 2
\end{pmatrix}-\begin{pmatrix}
2 & -1\\
1 & 0
\end{pmatrix} &= A \\
\begin{pmatrix}
-1-2 & 3-(-1)\\
0-1 & 2-0
\end{pmatrix} &= A \\
\begin{pmatrix}
-3 & 4 \\
-1 & 2
\end{pmatrix} &= A \\
(-3)(2)-(-1)(4) &= \left| A \right| \\
-2 &= \left| A \right|
\end{align} $
Dengan mengunakan sifat determinan matriks $\left| A^{-1} \right| = \dfrac{1}{\left | A \right |}$ dan $ |k \times A_{m\times m}| = k^m \times |A| $maka:
$\begin{align}
\left| 2 A^{-1} \right| &= 2^{2} \cdot \left| A^{-1} \right| \\
&= 2^{2} \cdot \dfrac{1}{\left | A \right |} \\
&= 4 \cdot \dfrac{1}{-2} \\
&= -2
\end{align} $
$\therefore$ Pilihan yang sesuai ialah $(B)\ -2$
30. Soal UTBK Tes Kompetensi Akademik SAINTEK 2019
Diketahui matriks $A$ berordo $2 \times 2$ dan matriks $B=\begin{pmatrix}
-3 & 5\\
-1 & 2
\end{pmatrix}$ dan $C=\begin{pmatrix}
4 & 5\\
2 & 3
\end{pmatrix}$. Jika $A$ memenuhi $B \cdot A=C$ maka determinan dari $\left( 2A^{-1} \right)$ adalah...
$\begin{align}
(A)\ & -2 \\
(B)\ & -1 \\
(C)\ & -\dfrac{1}{2} \\
(D)\ & \dfrac{1}{2} \\
(E)\ & 2
\end{align}$
Berdasarkan gosip pada perkalian matriks soal di atas dan menggunakan sifat determinan matriks yaitu $ \left|A \cdot B \right| = \left|A \right| \cdot \left| B \right|$ dan $ |k \times A_{m\times m}| = k^m \times |A|$, maka berlaku:
$\begin{align}
\left|B \right| &= \begin{vmatrix}
-3 & 5\\
-1 & 2
\end{vmatrix} \\
&= (-3)(2)-(-1)(5)=-1 \\
\left|C \right| &= \begin{vmatrix}
4 & 5\\
2 & 3
\end{vmatrix} \\
&= (4)(3)-(5)(2)=2 \\
\hline
B \cdot A &=C \\
\left|B \cdot A \right| &= \left| C \right| \\
\left|B \right| \cdot \left| A \right| &= \left| C \right| \\
-1 \cdot \left| A \right| &= 2 \\
\left| A \right| &= -2 \\
\hline
\left| 2 A^{-1} \right| &= 2^{2} \cdot \left| A^{-1} \right| \\
&= 2^{2} \cdot \dfrac{1}{\left | A \right |} \\
&= 4 \cdot \dfrac{1}{-2} \\
&= -2
\end{align} $
$\therefore$ Pilihan yang sesuai ialah $(A)\ -2$
31. Soal UTBK Tes Kompetensi Akademik SAINTEK 2019
Diketahui matriks $B=\begin{pmatrix}
2 & -1\\
-3 & 2
\end{pmatrix}$ dan $C=\begin{pmatrix}
-7 & 2\\
0 & 4
\end{pmatrix}$. Jika matriks $A$ berukuran $2 \times 2$ dan memenuhi persamaan $A^{3}+B=C$, maka determinan matriks $3 A^{-1}$ adalah...
$\begin{align}
(A)\ & -3 \\
(B)\ & -2 \\
(C)\ & -1 \\
(D)\ & 1 \\
(E)\ & 2
\end{align}$
Berdasarkan gosip pada penjumlahan matriks soal di atas dan menggunakan sifat determinan matriks yaitu $ |k \times A_{m\times m}| = k^m \times |A|$, maka berlaku:
$\begin{align}
A^{3}+B &= C \\
A^{3} &= C-B \\
&= \begin{pmatrix}
-7 & 2\\
0 & 4
\end{pmatrix} - \begin{pmatrix}
2 & -1\\
-3 & 2
\end{pmatrix} \\
&= \begin{pmatrix}
-7-2 & 2-(-1)\\
0+3 & 4-2
\end{pmatrix} \\
&= \begin{pmatrix}
-9 & 3 \\
3 & 2
\end{pmatrix} \\
\hline
\left| A^{3} \right| &= (-9)(2)-(3)(3) \\
\left| A \right|^{3} &= -27 \\
\left| A \right| &= -3 \\
\hline
\left| 3 A^{-1} \right| &= 3^{2} \cdot \left| A^{-1} \right| \\
&= 9 \cdot \dfrac{1}{-3} \\
&= -3
\end{align} $
$\therefore$ Pilihan yang sesuai ialah $(A)\ -3$
32. Soal UTBK Tes Kompetensi Akademik SAINTEK 2019
Diketahui matriks $A=\begin{pmatrix}
2 & 1\\
3 & 5
\end{pmatrix}$ mempunyai kekerabatan dengan matriks $B=\begin{pmatrix}
-5 & 3\\
1 & -2
\end{pmatrix}$. Matriks $C=\begin{pmatrix}
3 & 2\\
1 & -5
\end{pmatrix}$ dan matriks $D$ mempunyai kekerabatan yang serupa dengan $A$ dan $B$. Bentuk $C+D=\cdots$
$\begin{align}
(A)\ & \begin{pmatrix}
8 & 3\\
3 & -8
\end{pmatrix} \\
(B)\ & \begin{pmatrix}
8 & 3\\
3 & -2
\end{pmatrix} \\
(C)\ & \begin{pmatrix}
5 & 1\\
2 & -3
\end{pmatrix} \\
(D)\ & \begin{pmatrix}
3 & -2\\
-1 & -5
\end{pmatrix} \\
(E)\ & \begin{pmatrix}
-3 & 2\\
1 & 5
\end{pmatrix}
\end{align}$
Hubungan matriks:
$\begin{align}
A & \Leftrightarrow B \\
\begin{pmatrix}
2 & 1\\
3 & 5
\end{pmatrix} & \Leftrightarrow \begin{pmatrix}
-5 & 3\\
1 & -2
\end{pmatrix}
\end{align} $
Jika kita perhatikan kekerabatan kedua matriks di atas ialah unsur-unsur pada diagonal utama bertukar daerah kemudian dikalikan dengan $-1$ dan unsur-unsur pada diagonal samping bertukar tempat.
$\begin{align}
C & \Leftrightarrow D \\
\begin{pmatrix}
3 & 2\\
1 & -5
\end{pmatrix} & \Leftrightarrow \begin{pmatrix}
5 & 1\\
2 & -3
\end{pmatrix}\\
\hline
C + D &=
\begin{pmatrix}
3 & 2\\
1 & -5
\end{pmatrix}+\begin{pmatrix}
5 & 1\\
2 & -3
\end{pmatrix}\\
&=
\begin{pmatrix}
8 & 3\\
3 & -8
\end{pmatrix}
\end{align} $
$\therefore$ Pilihan yang sesuai ialah $(A)\ \begin{pmatrix}
8 & 3\\
3 & -8
\end{pmatrix}$
33. Soal UNBK Matematika IPS 2019 (*Soal Lengkap)
Suatu perusahaan konveksi memproduksi tiga model pakaian. Lama waktu pemotongan, penjahitan, dan finishing setiap potong pakaian disajikan dalam tabel berikut.
Jumlah waktu yang tersedia di pecahan pemotongan, penjahitan dan finishing disajikan dalam tabel berikut.
Lama Waktu Potong Jahit Finishing Model A 0,1 0,3 0,1 Model B 0,1 0,2 0,2 Model C 0,3 0,4 0,1
Jika banyak model pakaian yang akan diproduksi untuk model $A,\ B,\ \text{dan}\ C$ berturut-turut $x,\ y,\ \text{dan}\ z$, persamaan matriks yang sesuai untuk masalah tersebut adalah...
Pemotongan 68 Penjahitan 116 FinishingB 51
$ \begin{align}
(A)\ & \begin{pmatrix}
1 & 3 & 1\\
1 & 2 & 2 \\
3 & 4 & 1
\end{pmatrix}\begin{pmatrix}
x & y & z
\end{pmatrix}=\begin{pmatrix}
680 \\
1160 \\
510
\end{pmatrix} \\
(B)\ & \begin{pmatrix}
1 & 3 & 1\\
1 & 2 & 2 \\
3 & 4 & 1
\end{pmatrix}\begin{pmatrix}
x & y & z
\end{pmatrix}=\begin{pmatrix}
680 & 1160 & 510
\end{pmatrix} \\
(C)\ & \begin{pmatrix}
1 & 3 & 1\\
1 & 2 & 2 \\
3 & 4 & 1
\end{pmatrix}\begin{pmatrix}
x \\ y \\ z
\end{pmatrix}=\begin{pmatrix}
68 \\
116 \\
51
\end{pmatrix} \\
(D)\ & \begin{pmatrix}
1 & 1 & 3\\
3 & 2 & 4 \\
1 & 2 & 1
\end{pmatrix}\begin{pmatrix}
x \\ y \\ z
\end{pmatrix}=\begin{pmatrix}
680 \\
1160 \\
510
\end{pmatrix} \\
(E)\ & \begin{pmatrix}
1 & 3 & 1\\
1 & 2 & 2 \\
3 & 4 & 1
\end{pmatrix}\begin{pmatrix}
x \\ y \\ z
\end{pmatrix}=\begin{pmatrix}
680 \\
1160 \\
510
\end{pmatrix} \\
\end{align}$
Jika tabel pada soal kita gabungkan kurang lebih mirip berikut ini:
| Lama Waktu | Potong | Jahit | Finishing |
| Model A $(x)$ | 0,1 | 0,3 | 0,1 |
| Model B $(y)$ | 0,1 | 0,2 | 0,2 |
| Model C $(z)$ | 0,3 | 0,4 | 0,1 |
| Total Waktu | 68 | 116 | 51 |
- Waktu Pemotongan $0,1x+0,1y+0,3z=68$
$ x+ y+3z=680$ - Waktu Penjahitan $0,3x+0,2y+0,4z=116$
$ 3x+ 2y+ 4z=1160$ - Waktu Finishing $0,1x+0,2y+0,1z=116$
$ x+ 2y+ z=510$
$\begin{pmatrix}
1 & 1 & 3\\
3 & 2 & 4 \\
1 & 2 & 1
\end{pmatrix}\begin{pmatrix}
x \\ y \\ z
\end{pmatrix}=\begin{pmatrix}
680 \\
1160 \\
510
\end{pmatrix}$
Untuk membuktikan penulisan matriks di atas benar atau salah mampu dicoba dengan mencoba mengalikan matriks.
$\therefore$ Pilihan yang sesuai ialah $(D)\ \begin{pmatrix}
1 & 1 & 3\\
3 & 2 & 4 \\
1 & 2 & 1
\end{pmatrix}\begin{pmatrix}
x \\ y \\ z
\end{pmatrix}=\begin{pmatrix}
680 \\
1160 \\
510
\end{pmatrix}$
34. Soal UNBK Matematika IPS 2019 (*Soal Lengkap)
Diketahui matriks $A=\begin{pmatrix}
4 & -2 \\
1 & 5
\end{pmatrix}$, $B=\begin{pmatrix}
3 & 7 \\
-2 & -4
\end{pmatrix}$ dan $C=\begin{pmatrix}
7 & -9 \\
10 & -2
\end{pmatrix}$ memenuhi persamaan $X=A+2B-C^{T}$, dengan $C^{T}$ merupakan transpose matriks $C$. Invers matriks $X$ adalah...
$ \begin{align}
(A)\ & -\dfrac{1}{15} \begin{pmatrix}
-1 & 2 \\
-6 & 3
\end{pmatrix} \\
(B)\ & -\dfrac{1}{15} \begin{pmatrix}
-1 & -6 \\
-2 & 3
\end{pmatrix} \\
(C)\ & \dfrac{1}{15} \begin{pmatrix}
1 & 2 \\
6 & -3
\end{pmatrix} \\
(D)\ & \dfrac{1}{15} \begin{pmatrix}
1 & -2 \\
6 & 3
\end{pmatrix} \\
(E)\ & \dfrac{1}{15} \begin{pmatrix}
1 & -2 \\
-6 & -3
\end{pmatrix} \\
\end{align}$
$ \begin{align}
X = & A+2B-C^{T} \\
= & \begin{pmatrix}
4 & -2 \\
1 & 5
\end{pmatrix}+2\begin{pmatrix}
3 & 7 \\
-2 & -4
\end{pmatrix}-\begin{pmatrix}
7 & 10 \\
-9 & -2
\end{pmatrix} \\
= & \begin{pmatrix}
4 & -2 \\
1 & 5
\end{pmatrix}+\begin{pmatrix}
6 & 14 \\
-4 & -8
\end{pmatrix}-\begin{pmatrix}
7 & 10 \\
-9 & -2
\end{pmatrix} \\
= & \begin{pmatrix}
4+6-7 & -2+14-10 \\
1-4+9 & 5-8+2
\end{pmatrix} \\
= & \begin{pmatrix}
3 & 2 \\
6 & -1
\end{pmatrix}
\end{align}$
$ \begin{align}
X^{-1} = & \dfrac{1}{(3)(-1)-(-2)(-6)} \begin{pmatrix}
-1 & -2 \\
-6 & 3
\end{pmatrix} \\
= & \dfrac{1}{-3-12} \begin{pmatrix}
-1 & -2 \\
-6 & 3
\end{pmatrix} \\
= & -\dfrac{1}{15} \begin{pmatrix}
-1 & -2 \\
-6 & 3
\end{pmatrix}
\end{align}$
$\therefore$ Pilihan yang sesuai ialah $(B)\ -\dfrac{1}{15} \begin{pmatrix}
-1 & -6 \\
-2 & 3
\end{pmatrix}$
35. Soal UNBK Matematika IPS 2019 (*Soal Lengkap)
Diketahui matriks $A=\begin{pmatrix}
4x-y & -2 \\
z & 4
\end{pmatrix}$, $B=\begin{pmatrix}
2 & y+2 \\
1 & z-x
\end{pmatrix}$ dan $C=\begin{pmatrix}
4 & 8 \\
-10 & 10
\end{pmatrix}$ dan $C^{T}$ ialah transpose matriks $C$. Jika $3A-B=C^{T}$, nilai dari $-3x+y+5z$ adalah...
$ \begin{align}
(A)\ & 8 \\
(B)\ & 10 \\
(C)\ & 14 \\
(D)\ & 16 \\
(E)\ & 20 \\
\end{align}$
$ \begin{align}
C^{T} = & 3A-B \\
\begin{pmatrix}
4 & -10 \\
8 & 10
\end{pmatrix} = & 3\begin{pmatrix}
4x-y & -2 \\
z & 4
\end{pmatrix}-\begin{pmatrix}
2 & y+2 \\
1 & z-x
\end{pmatrix} \\
\begin{pmatrix}
4 & -10 \\
8 & 10
\end{pmatrix} = & \begin{pmatrix}
12x-3y & -6 \\
3z & 12
\end{pmatrix}-\begin{pmatrix}
2 & y+2 \\
1 & z-x
\end{pmatrix} \\
\begin{pmatrix}
4 & -10 \\
8 & 10
\end{pmatrix} = & \begin{pmatrix}
12x-3y-2 & -6-y-2 \\
3z-1 & 12-z+x
\end{pmatrix}
\end{align}$
Dari kesamaan dua matrks di atas kita peroleh:
- $-6-y-2=-10$ sehingga $y=2$
- $3z-1=8$ sehingga $z=3$
- $12-z+x=10$ sehingga $x=1$
- Nilai $-3x+y+5z$ ialah $-3(1)+(2)+5(3)=-3+2+15=14$
$\therefore$ Pilihan yang sesuai ialah $(B)\ 14$
36. Soal Matematika Dasar SIMAK UI 2019 Kode 539 (*Soal Lengkap)
Diketahui $A=\begin{pmatrix}
1 & 2\\
2 & 1
\end{pmatrix}$ dan $B=\begin{pmatrix}
-1 & 2\\
1 & 1
\end{pmatrix}$. Jika $A+tB$ merupakan matriks singular, nilai $t^{2}+3t+2$ adalah...
$\begin{align}
(A)\ & 0 \\
(B)\ & 1 \\
(C)\ & 2 \\
(D)\ & 3 \\
(E)\ & 5
\end{align}$
$ \begin{align}
A+tB &= \begin{pmatrix}
1 & 2\\
2 & 1
\end{pmatrix}+t\begin{pmatrix}
-1 & 2\\
1 & 1
\end{pmatrix} \\
&= \begin{pmatrix}
1 & 2\\
2 & 1
\end{pmatrix}+ \begin{pmatrix}
-t & 2t\\
t & t
\end{pmatrix} \\
&= \begin{pmatrix}
1-t & 2+2t\\
2+t & 1+t
\end{pmatrix} \\
0&= \begin{vmatrix}
1-t & 2+2t\\
2+t & 1+t
\end{vmatrix} \\
0&= \left( 1-t^{2}\right)-\left(4+6t+2t^{2}\right) \\
0&= -3t^{2}-6t-3 \\
0&= t^{2}+2t+1 \\
0&= \left(t+1 \right)^{2} \\
& t=-1 \\
t^{2}+3t+2 &= (-1)^{2}+3(-1)+2 \\
&= 0 \\
\end{align} $
$\therefore$ Pilihan yang sesuai ialah $(A)\ 0$
Jika engkau tidak mampu menahan lelahnya belajar, Maka engkau harus menanggung pahitnya kebodohan ___pythagorasBeberapa pembahasan soal Matematika Dasar Matriks (*Soal Dari Berbagai Sumber) di atas ialah coretan kreatif siswa pada
- lembar jawaban penilaian harian matematika,
- lembar jawaban penilaian tamat semester matematika,
- presentasi hasil diskusi matematika atau
- pembahasan quiz matematika di kelas.
Jangan Lupa Untuk Berbagi 🙏Share is Caring 👀 dan JADIKAN HARI INI LUAR BIASA! - WITH GOD ALL THINGS ARE POSSIBLE😊
Video pilihan khusus untuk Anda 😂 Masih menganggap matematika hanya hitung-hitungan semata, mari kita lihat kreativitas siswa ini;

Belum ada Komentar untuk "Bank Soal Dan Pembahasan Matematika Dasar Matriks"
Posting Komentar